8553. Computer network
A computer network comprises n
computers, numbered from 0 to n – 1.
Each one, after receiving a message, passes it to some other computers. If a
message from computer x can
reach a computer y,
this does not necessarily mean that a message from computer y reaches the computer x. The system administrators want to
determine the minimum number of computers from which a message has to be sent
in order to reach all the computers in the network.
For better transmission of messages, they believe that the network needs
to be extended by adding new connections between some computers, so when
sending a message from an arbitrary computer it will be distributed to all
others. For this purpose, it is necessary to determine the minimum number of
new connections to be added, so that each of the computers can be used as initial for distribution of messages.
Write a program cnet that finds the minimal
number of computers from which a message needs to be sent in order to be
distributed to all computers in the network and finds the minimum number of new
connections that need to be added, in order to allow a message,
sent from each of the computers, to reach every other computer in the network.
Input. The first line
contains two integers n (1 ≤ n ≤ 1600) and m (0 ≤ m ≤ 120000), representing the number of computers and the number of connections
between them. Each of the next m lines
describe one available connection. The first number is the number of the computer sending the message, and the second number
is the number of the computer receiving the message.
Output. On a single line
print two integers – the minimum number of computers that are used as initial
for distributing a message to the whole network and the minimum number of
additional connections needed to extend the network in a way that a message
sent from an arbitrary chosen computer, will reach all the others.
|
Sample
input 1 |
Sample
output 1 |
|
5 6 0 1 0 3 0 2 1 3 1 4 4 0 |
1 2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 12 0 1 0 2 1 0 1 2 2 0 2 1 3 4 3 5 4 3 4 5 5 3 5 4 |
2 2 |
SOLUTION
graphs – strongly
connected components
Algorithm analysis
Find the strongly connected components in the graph. If there is one
component (the graph is strongly connected), then a message for the entire
network can be sent from any one computer, and the number of additional
connections required is 0.
Let the graph be not strongly connected.
Consider its condensation. For each connected component, find out whether there
are outgoing and incoming edges. If some component does not have incoming
edges, then in order to send a message to entire network, the message must be
sent from a vertex belonging to this component. For the condensation below, the
message should be sent from 3 computers.
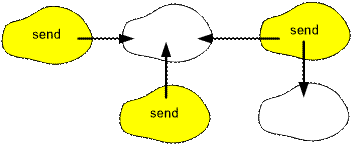
The message can be
passed from any computer to any other in the network only if the graph is
strongly connected. The minimum number of edges should be added to the original
graph in such way as to make it strongly connected.
For each connected component there must be both an incoming and outgoing edge.
Let:
ñ1 is the number of components
without incoming edges (on the picture ñ1
= 3);
ñ2 is the number of components
without outgoing edges (on the picture ñ2
= 2);
Then its always possible to add max(ñ1, ñ2)
edges to make the graph strongly connected. For our example max(ñ1, ñ2) = max(3, 2) = 3. To get a strongly connected graph,
it is enough to add 3 edges.
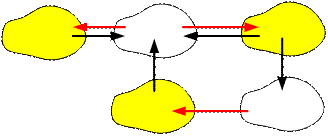
Example
In the first test case the graph contains three strongly connected
components.
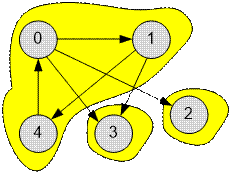
There is one
component that has no incoming edges: {0, 1, 4}, ñ1 = 1;
There are two
components that has no outgoing edges: {2}, {3}, ñ2 = 2;
The message that should be distributed throughout the network,
must be sent from components that have no incoming edges. We have one such
component. The mailing can be done from one vertex (0, 1 or 4).
In order for the whole graph to become strongly connected, it is
necessary to create edges outgoing from vertices 2 and 3, and at least one of the
edges must be incoming into the component consisting of vertices {0, 1, 4}. For
example, creating the following edges will make the graph strongly connected:
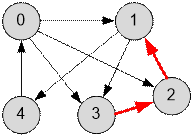
Algorithm
realization
The
input graph is stored in the adjacency list g.
The reverse graph (the graph where all edge directions are reversed) is stored
in the adjacency list gr. Declare
also some additional arrays.
vector<vector<int> > g, gr;
vector<int> used, top, color;
vector<int> in, out;
The function dfs1 implements depth first search on the input graph. In the array top store the
vertices in the order in which the depth first search ends their
processing.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs1(to);
top.push_back(v);
}
The function dfs2 implements
depth first search on the reversed graph. All vertices that will
be traversed as a result of a recursive call of dfs2 function
belong to one strongly connected component. Color all
the visited vertices with color c.
void dfs2(int v, int c)
{
color[v] = c;
for (int to : gr[v])
if (color[to] == -1) dfs2(to, c);
}
The main part of the program. Read the input
data. Build the reversed graph.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
gr.resize(n
+ 1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
gr[b].push_back(a);
}
Start the depth first
search on the input graph. The sequence in which the graph
vertices processing is completed is stored in the array top.
used.resize(n);
for (i = 0; i < n; i++)
if (!used[i]) dfs1(i);
Start the depth first search on the reversed
graph. Iterate the vertices of the reversed graph in the order of
traversing the array top from right to left (from end
to start). The vertices included in one strongly connected component
are colored with the same color. The current color is in the variable c.
color.assign(n,
-1);
reverse(top.begin(),
top.end());
c = 0;
for (int v : top)
if (color[v] == -1) dfs2(v, c++);
The variable c
contains the number of connected components. Set in[i] = 1 if there is no incoming edge to the connected component
number i (and in[i] = 0 otherwise). Set out[i]
= 1 if there is no outgoing edge from the connected component number i (and out[i] = 0 otherwise).
in.assign(c, 1);
out.assign(c, 1);
for (i = 0; i < g.size(); i++)
for (int to : g[i])
If an edge i
→ to connects different
connected components, then component number color[to] has an incoming edge, and component number color[i] has an outgoing edge.
if (color[i] != color[to])
{
in[color[to]] = 0;
out[color[i]] = 0;
}
Count the number of components that do not have incoming (ñ1) and outgoing (ñ2) edges.
c1
= c2 = 0;
for (i = 0; i < in.size(); i++)
{
if (in[i]) c1++;
if (out[i]) c2++;
}
Compute and print the answer.
if (c == 1) ans = 0; else ans = max(c1, c2);
printf("%d %d\n", c1, ans);
Java realization
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g, gr;
static int used[], color[], in[], out[];
static Vector<Integer> top = new Vector<Integer>();
static void
dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 0) dfs1(to);
}
top.add(v);
}
static void
dfs2(int v, int c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to = gr[v].get(i);
if (color[to] == -1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n];
for(int i = 0; i < n; i++)
g[i] = new
ArrayList<Integer>();
gr = new ArrayList[n];
for(int i = 0; i < n; i++)
gr[i] = new
ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n];
for(int i = 0; i < n; i++)
if (used[i] == 0) dfs1(i);
color = new int[n];
Arrays.fill(color, -1);
int c = 0;
for(int i = 0; i < n; i++)
{
int v = top.get(n-i-1);
if (color[v] == -1) dfs2(v,c++);
}
in = new int[c];
Arrays.fill(in, 1);
out = new int[c];
Arrays.fill(out, 1);
for(int i = 0; i < g.length; i++)
for(int j = 0; j < g[i].size(); j++)
{
int to = g[i].get(j);
// check edge i -> j if they in the same scc.
if (color[i] != color[to])
{
in[color[to]] = 0;
out[color[i]] = 0;
}
}
int c1 = 0, c2 = 0;
for(int i = 0; i < in.length; i++)
{
if (in[i] == 1) c1++;
if (out[i] == 1) c2++;
}
int ans = 0;
if (c != 1) ans
= Math.max(c1,c2);
System.out.println(c1 + " " + ans);
con.close();
}
}